Proof of Optimal Error Scaling for ESPRIT Algorithm

Table of Links

Abstract and 1 Introduction

1.1 ESPRIT algorithm and central limit error scaling

1.2 Contribution

1.3 Related work

1.4 Technical overview and 1.5 Organization

2 Proof of the central limit error scaling

3 Proof of the optimal error scaling

4 Second-order eigenvector perturbation theory

5 Strong eigenvector comparison

5.1 Construction of the “good” P

5.2 Taylor expansion with respect to the error terms

5.3 Error cancellation in the Taylor expansion

5.4 Proof of Theorem 5.1

A Preliminaries

B Vandermonde matrice

C Deferred proofs for Section 2

D Deferred proofs for Section 4

E Deferred proofs for Section 5

F Lower bound for spectral estimation

References

3 Proof of the optimal error scaling

In this section, we present the formal statement of our main result (Theorem 1.4) and the proof.

Theorem 3.1 (Optimal error scaling of ESPRIT, formal version of Theorem 1.4). Consider the spectral estimation problem under assumptions Eq. (1.3) and Eq. (1.4). Assume α > 1 and

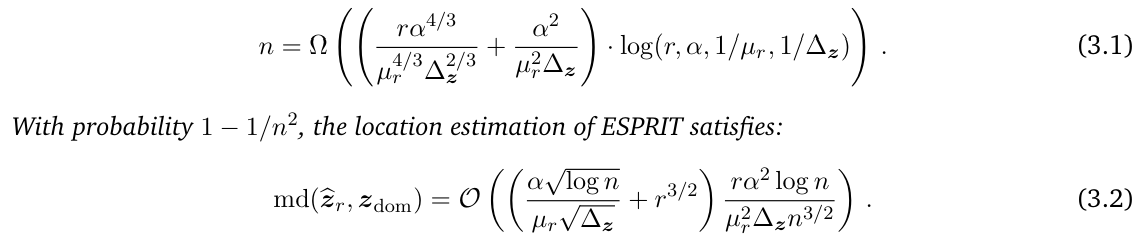
If we further assume

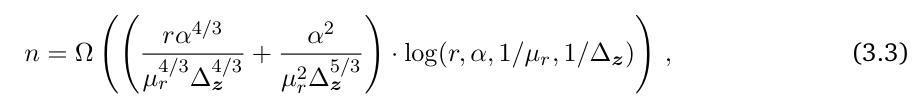
then the location estimation satisfies:

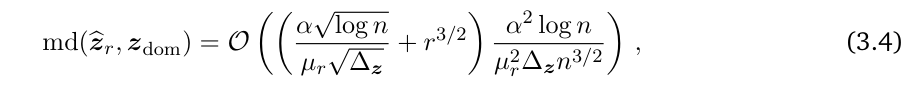
and the intensity estimation of ESPRIT satisfies:

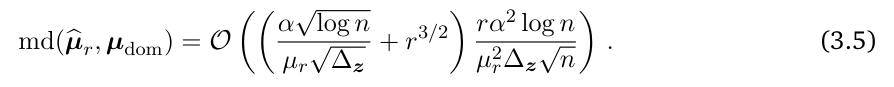
Note that the permutation in the definition of the matching distance is the same for both Eqs. (3.4) and (3.5).

Proof of Theorem 3.1. We prove the error scaling of the location estimation and intensity estimation of the ESPRIT algorithm below.

Then, by Eq. (2.3) in Lemma 2.2, we obtain that

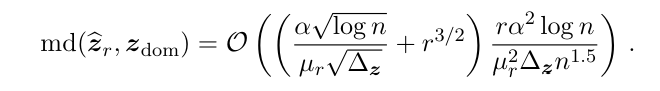
The first location estimation guarantee (Eq. (3.2)) is proved.

If we further assume that a stronger condition on n (Eq. (3.3)) holds, then by Eq. (3.6), we have

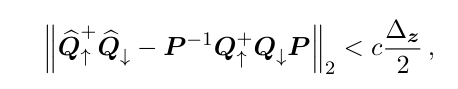
where c ∈ (0, 1) that satisfies the condition (Eq. (2.4)) in Lemma 2.2. By Eq. (2.5), we obtain that

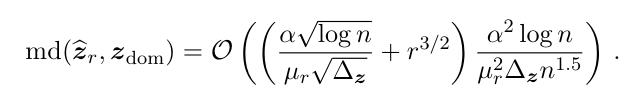
The second location estimation guarantee (Eq. (3.4)) is proved.

For the first term in Eq. (3.7), we have

Plugging Eqs. (3.10) and (3.11) back into Eq. (3.9), we obtain

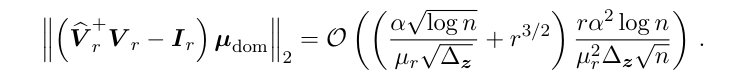
For the second term in Eq. (3.7), using Eq. (3.8) and a similar proof as Proposition C.3, we have