Table of Links
1.1 ESPRIT algorithm and central limit error scaling
1.4 Technical overview and 1.5 Organization
2 Proof of the central limit error scaling
3 Proof of the optimal error scaling
4 Second-order eigenvector perturbation theory
5 Strong eigenvector comparison
5.1 Construction of the “good” P
5.2 Taylor expansion with respect to the error terms
5.3 Error cancellation in the Taylor expansion
C Deferred proofs for Section 2
D Deferred proofs for Section 4
E Deferred proofs for Section 5
F Lower bound for spectral estimation
A Preliminaries
A.1 Notation

A.2 Pseudoinverses
We will make frequent use of the (Moore–Penrose) pseudoinverse:

We will make use of the reverse order for the pseudoinverse [Gre66]:

Perturbation theory for pseudoinverses is provided by the following theorem [Han87, eq. (21)]:

A.3 Matrix norms

The result is proven.
A.4 Neumann series
The Neumann series is one of the most powerful tools in matrix analysis. It is the matrix generalization of a geometric series.
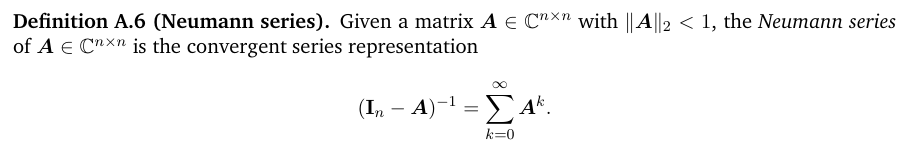
A.5 Eigenvalue and eigenvector perturbation theory
Our argument will require several standard results from matrix perturbation theory. First, we will make use of additive and multiplicative perturbation theorems for eigenvalues of Hermitian matrices. For additive perturbation, we will use Weyl’s theorem:
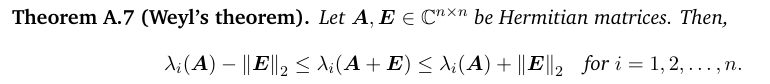
For multiplicative perturbation theory, we will use Ostrowski’s theorem.

Ostrowski’s theorem for the case in which A and B are both square appears in [HJ12, Thm. 4.5.9]. The generalization to B rectangular presented here is straightforward.
Next, we will need perturbation bounds of eigenspaces of Hermitian matrices. The classical measure of the distance between subspaces is the principal angle, which admits multiple equivalent definitions [SS90, Sec. I.5]. We use the following definition: for matrices U and V with orthonormal columns, the sin of the principal angle between the ranges of U and V is
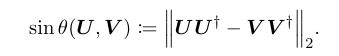
With this definition in hand, we now state the classical result for the perturbation of eigenspaces of Hermitian matrices, due to a Davis and Kahan [DK70, sin θ theorem]:

Last, we will need one result for the perturbation of diagonalizable matrices, a version of the famous Bauer–Fike theorem augmented by Gerschgorin and Ostrowski’s continuity argument. We take this result from [SS90]:
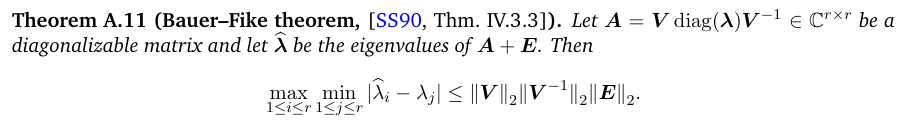
Moreover, we have the following bound in the optimal matching distance, defined in Eq. (1.9):
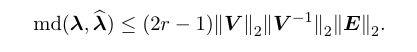
A.6 Spectral perturbation via resolvents

We first state a lemma that estimates the locations of the perturbed eigenvalues via the resolvent method.

Next, we present the following results that express the spectral projector as the contour integral of the resolvent:

that is uniformly convergent on C. Therefore, integrating both sides we obtain
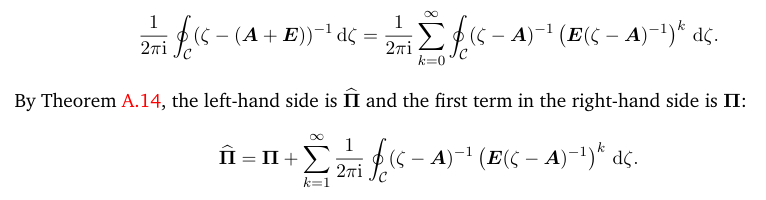
This is the stated conclusion.
This paper is available on arxiv under CC BY 4.0 DEED license.
Authors:
(1) Zhiyan Ding, Department of Mathematics, University of California, Berkeley;
(2) Ethan N. Epperly, Department of Computing and Mathematical Sciences, California Institute of Technology, Pasadena, CA, USA;
(3) Lin Lin, Department of Mathematics, University of California, Berkeley, Applied Mathematics and Computational Research Division, Lawrence Berkeley National Laboratory, and Challenge Institute for Quantum Computation, University of California, Berkeley;
(4) Ruizhe Zhang, Simons Institute for the Theory of Computing.

